- 全部分类/
- 教育教学/
- 数理天地(初中版)
 扫码免费借阅
扫码免费借阅
目录
快速导航-
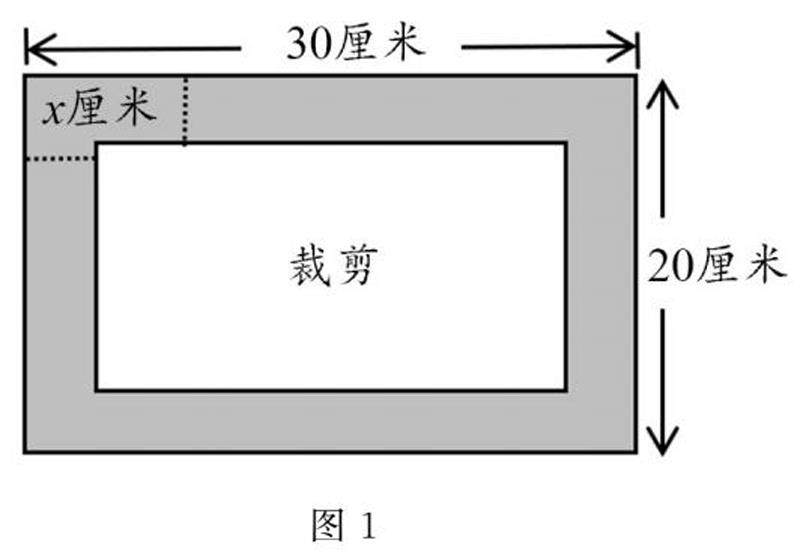
基础精讲 | 一元二次方程在面积问题中的应用
基础精讲 | 一元二次方程在面积问题中的应用
-

基础精讲 | 设参求值在反比例函数问题中的应用
基础精讲 | 设参求值在反比例函数问题中的应用
-

基础精讲 | 二次函数在实际问题中的应用例析
基础精讲 | 二次函数在实际问题中的应用例析
-

基础精讲 | 提升科学思维
基础精讲 | 提升科学思维
-

基础精讲 | 初中数学因式分解方法与例题解析
基础精讲 | 初中数学因式分解方法与例题解析
-

基础精讲 | 初中数学二次函数最值问题的题型分析与总结
基础精讲 | 初中数学二次函数最值问题的题型分析与总结
-

基础精讲 | 几何背景下的线段最值模型探究指导
基础精讲 | 几何背景下的线段最值模型探究指导
-
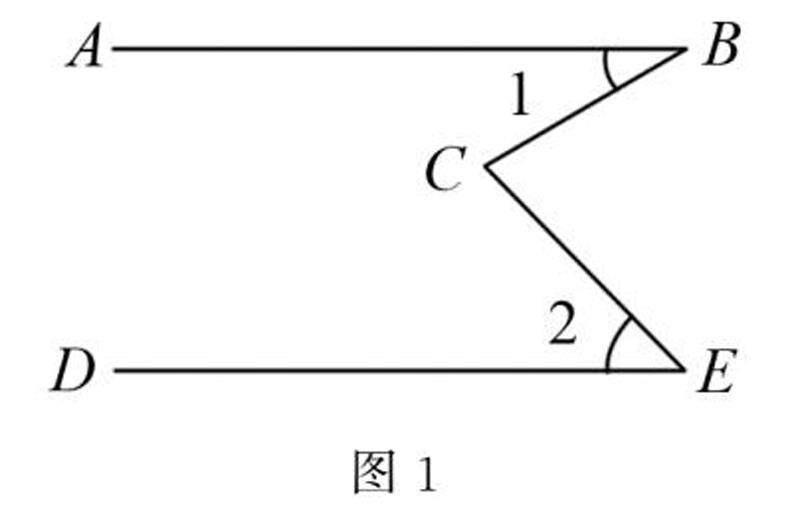
基础精讲 | 初中数学平行线问题中辅助线的应用
基础精讲 | 初中数学平行线问题中辅助线的应用
-

基础精讲 | 三角形面积公式在不同问题中的应用分析
基础精讲 | 三角形面积公式在不同问题中的应用分析
-

基础精讲 | 新函数图象与性质探讨
基础精讲 | 新函数图象与性质探讨
-

基础精讲 | “几何法+勾股定理”破解路径问题探究
基础精讲 | “几何法+勾股定理”破解路径问题探究
-

基础精讲 | 基于新课标的初中数学几何直观的培养
基础精讲 | 基于新课标的初中数学几何直观的培养
-

例题精讲 | 初中数学一例典型试题的解题步骤分析
例题精讲 | 初中数学一例典型试题的解题步骤分析
-
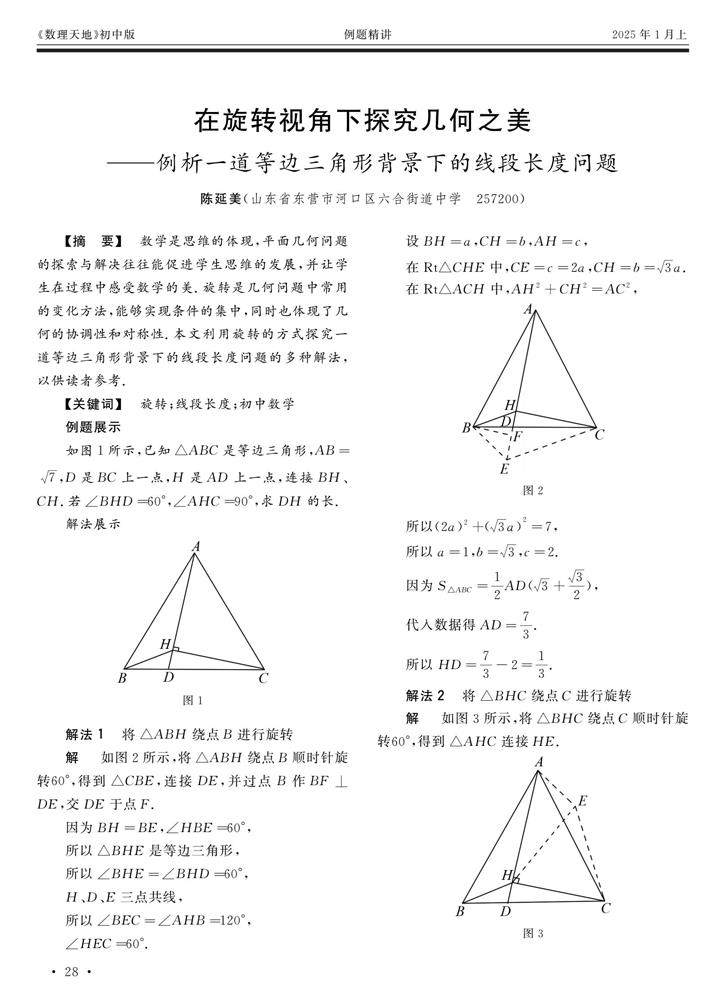
例题精讲 | 在旋转视角下探究几何之美
例题精讲 | 在旋转视角下探究几何之美
-

例题精讲 | 巧构倍(半)角,妙求线段比
例题精讲 | 巧构倍(半)角,妙求线段比
-

例题精讲 | 巧构双直角,妙求线段长
例题精讲 | 巧构双直角,妙求线段长
-

例题精讲 | 例析“1/a+1/b=1/c”型问题的证明方法
例题精讲 | 例析“1/a+1/b=1/c”型问题的证明方法
-

例题精讲 | 巧借中点条件,合理联想构造
例题精讲 | 巧借中点条件,合理联想构造
-

例题精讲 | 巧用等分点,妙解三连比
例题精讲 | 巧用等分点,妙解三连比
-

例题精讲 | 例谈任务型学习在初中数学教学中的应用
例题精讲 | 例谈任务型学习在初中数学教学中的应用
-

例题精讲 | 例析初中数学跨学科任务教学的优化
例题精讲 | 例析初中数学跨学科任务教学的优化
-

例题精讲 | 巧用截长补短法证明线段之间的数量关系
例题精讲 | 巧用截长补短法证明线段之间的数量关系
-

例题精讲 | 学科核心素养下的初中数学开放性试题开发
例题精讲 | 学科核心素养下的初中数学开放性试题开发
-

解题技巧 | 含字母系数方程的解法
解题技巧 | 含字母系数方程的解法
-

解题技巧 | 刍议递推法在初中数学解题中的应用
解题技巧 | 刍议递推法在初中数学解题中的应用
-

解题技巧 | 转化思想在初中数学解题中的应用与实践
解题技巧 | 转化思想在初中数学解题中的应用与实践
-
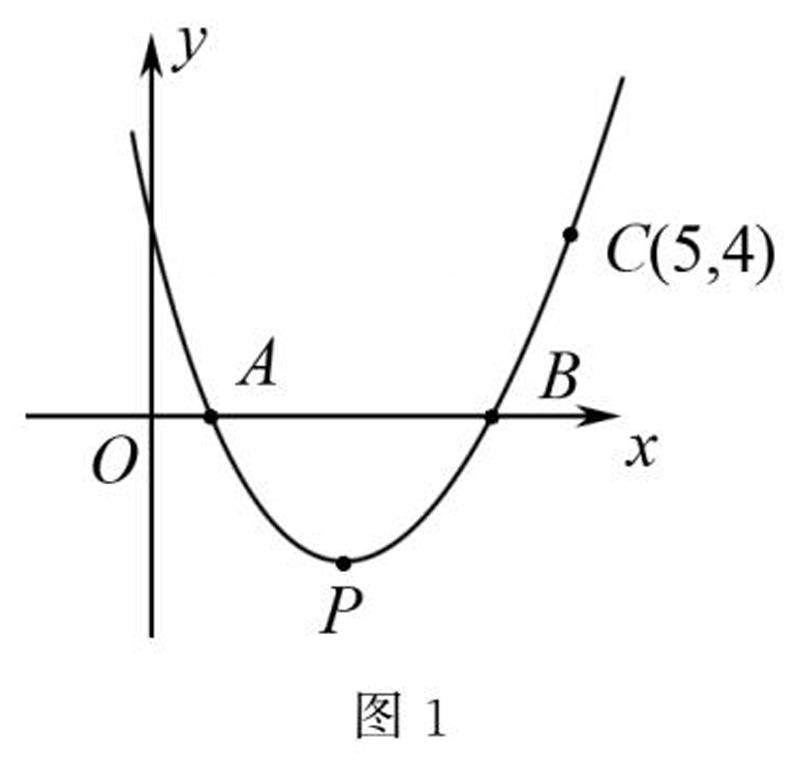
解题技巧 | 初中数学函数应用题解题技巧
解题技巧 | 初中数学函数应用题解题技巧
-
解题技巧 | 初中数学因式分解中的常见方法及例题解析
解题技巧 | 初中数学因式分解中的常见方法及例题解析
-

解题技巧 | 二次函数中几何最值问题的求解策略
解题技巧 | 二次函数中几何最值问题的求解策略
-
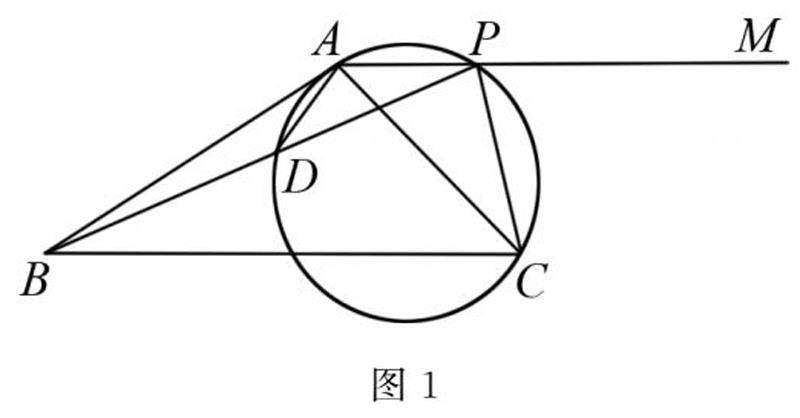
解题技巧 | 初中数学圆中最值问题解题技巧的探究
解题技巧 | 初中数学圆中最值问题解题技巧的探究
-

解题技巧 | 平面直角坐标系中点的规律性问题解法探析
解题技巧 | 平面直角坐标系中点的规律性问题解法探析
-

解题技巧 | 利用倍长中线法巧解几何题
解题技巧 | 利用倍长中线法巧解几何题
-

解题技巧 | 特殊四边形动点问题的解题策略
解题技巧 | 特殊四边形动点问题的解题策略
-

解题技巧 | “构造辅助圆”在初中数学解题中的灵活运用
解题技巧 | “构造辅助圆”在初中数学解题中的灵活运用
-
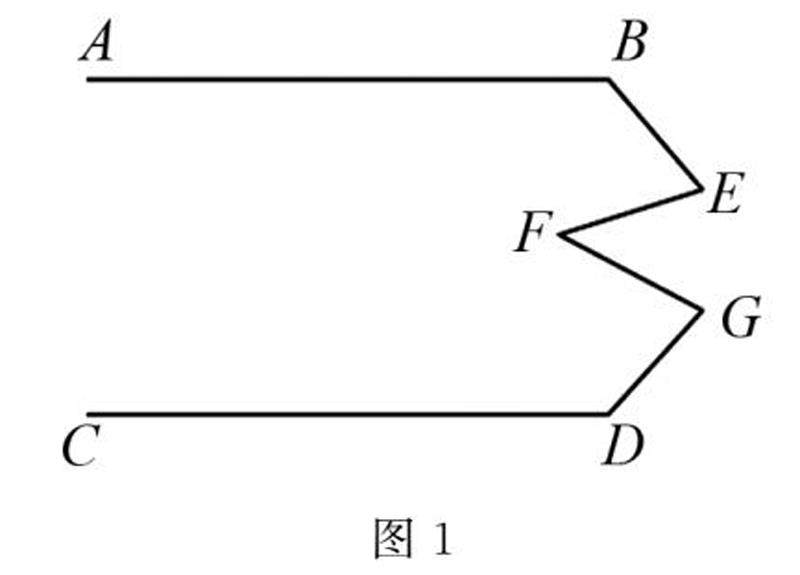
解题技巧 | 平行线中有关拐点问题的解题技巧
解题技巧 | 平行线中有关拐点问题的解题技巧
-
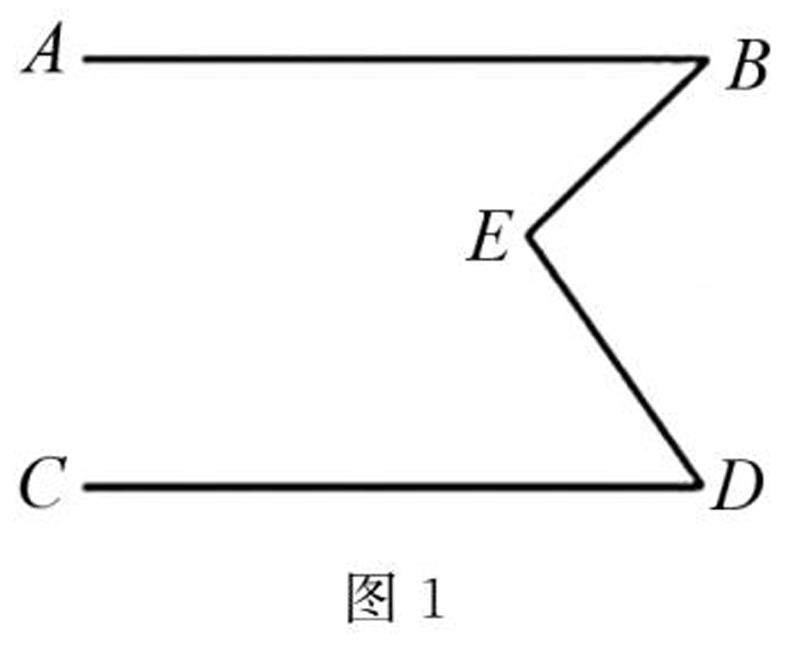
解题技巧 | 与平行线相关的三大模型探究
解题技巧 | 与平行线相关的三大模型探究
-
聚焦“双减” | “双减”背景下初中数学课后服务实效性研究
聚焦“双减” | “双减”背景下初中数学课后服务实效性研究
-
聚焦“双减” | “双减”背景下初中数学教学提质增效策略探究
聚焦“双减” | “双减”背景下初中数学教学提质增效策略探究
-
聚焦“双减” | “双减”背景下的农村初中数学作业分层设计策略研究
聚焦“双减” | “双减”背景下的农村初中数学作业分层设计策略研究
-
优化课堂方法 | 初中数学大单元教学的思考与探究
优化课堂方法 | 初中数学大单元教学的思考与探究
-
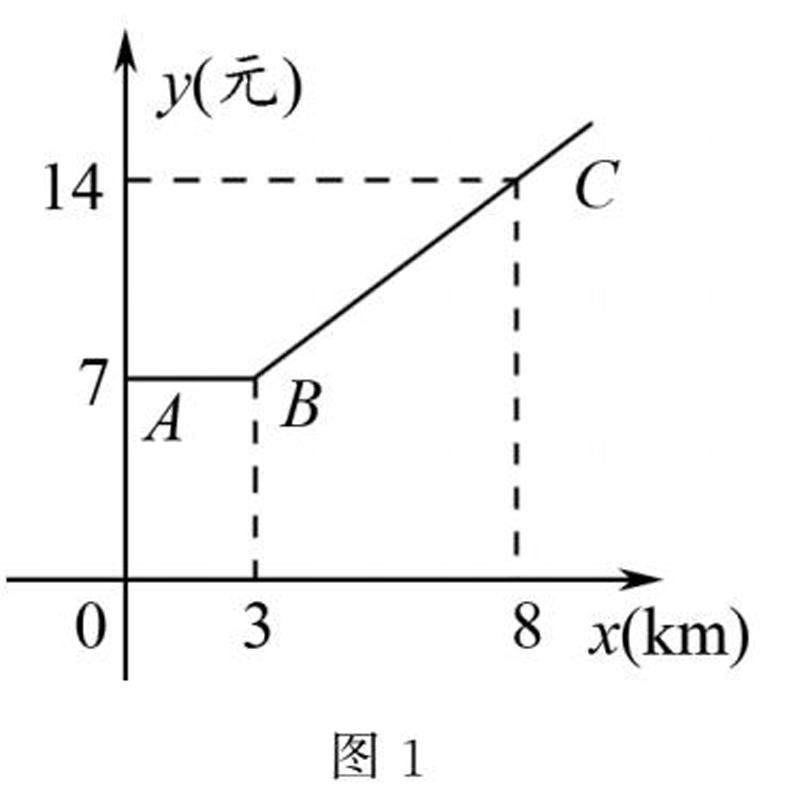
优化课堂方法 | 大概念视角下初中数学单元复习教学的实践与思考
优化课堂方法 | 大概念视角下初中数学单元复习教学的实践与思考
-
优化课堂方法 | 用多元化策略提升初中数学教学质量的探究
优化课堂方法 | 用多元化策略提升初中数学教学质量的探究
-
优化课堂方法 | 问题串在初中数学教学中的运用
优化课堂方法 | 问题串在初中数学教学中的运用
-
优化课堂方法 | 初中数学单元整体模块教学策略
优化课堂方法 | 初中数学单元整体模块教学策略
-
优化课堂方法 | 教学评一体化模式下初中数学教学实践探讨
优化课堂方法 | 教学评一体化模式下初中数学教学实践探讨
-
优化课堂方法 | 初中数学大单元结构化授课论述
优化课堂方法 | 初中数学大单元结构化授课论述
-

教学思想实践 | 立足课堂教学培养运算能力
教学思想实践 | 立足课堂教学培养运算能力
-
教学思想实践 | 数学建模思想在初中数学教学中的融入路径探究
教学思想实践 | 数学建模思想在初中数学教学中的融入路径探究
-
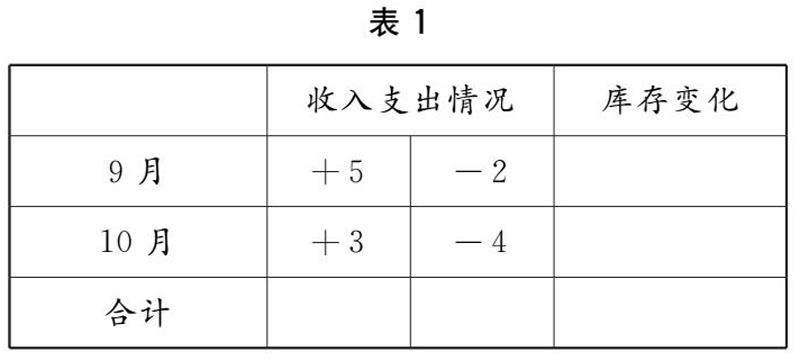
教学思想实践 | 数形结合思想在初中数学课堂中的运用策略研究
教学思想实践 | 数形结合思想在初中数学课堂中的运用策略研究
-
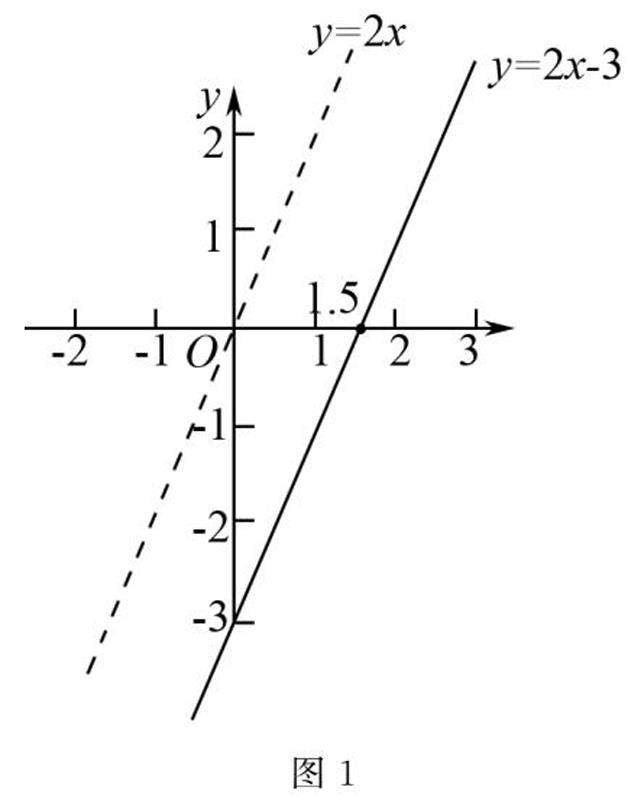
教学思想实践 | 初中数学数形结合教学策略与学生思维发展
教学思想实践 | 初中数学数形结合教学策略与学生思维发展
-
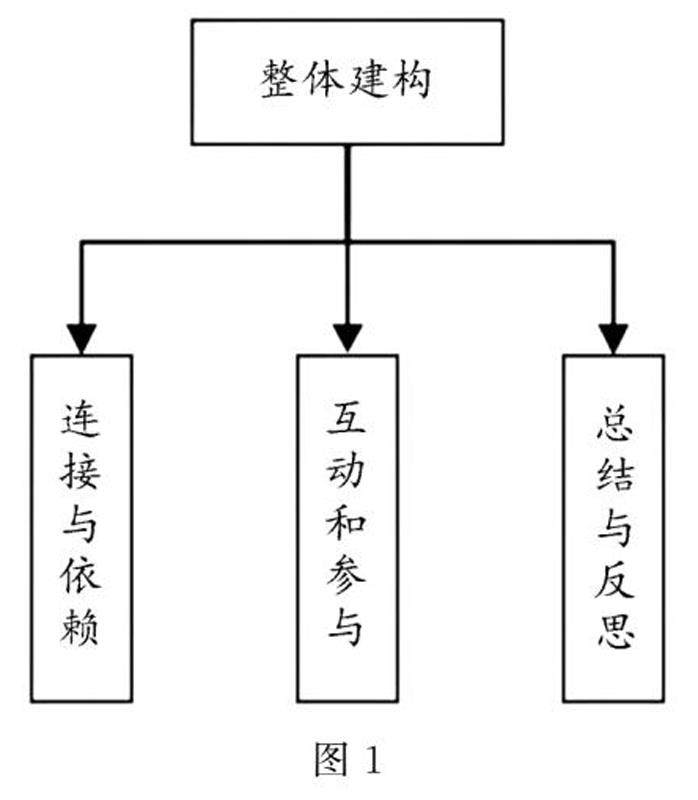
教学思想实践 | 整体建构理念下“图形与几何”大单元教学研究
教学思想实践 | 整体建构理念下“图形与几何”大单元教学研究
-
教学思想实践 | 初中数学单元整体教学设计与实施策略
教学思想实践 | 初中数学单元整体教学设计与实施策略
-
教学思想实践 | 运用导学案促进初中数学深度学习的研究
教学思想实践 | 运用导学案促进初中数学深度学习的研究
-
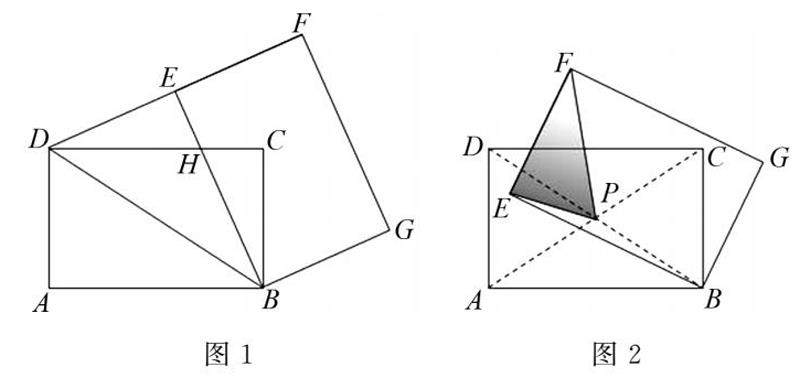
教学经验交流 | “相对与绝对”哲学思想在初中数学教学中的价值
教学经验交流 | “相对与绝对”哲学思想在初中数学教学中的价值
-

教学经验交流 | “平面内点的坐标”教学设计
教学经验交流 | “平面内点的坐标”教学设计
-
教学经验交流 | 数学游戏在初中数学教学中的作用及实施途径
教学经验交流 | 数学游戏在初中数学教学中的作用及实施途径
-
教学经验交流 | 新中考背景下谈初中数学教学改革
教学经验交流 | 新中考背景下谈初中数学教学改革
-
教学经验交流 | 新课标视域下初中数学后进生的转化策略探究
教学经验交流 | 新课标视域下初中数学后进生的转化策略探究
-
核心素养培养 | 指向学生解题能力提升的初中数学教学实践
核心素养培养 | 指向学生解题能力提升的初中数学教学实践
-

核心素养培养 | 基于核心素养的试题命制的实践与启发
核心素养培养 | 基于核心素养的试题命制的实践与启发
-
核心素养培养 | 浅谈初中数学教学中学生核心素养的发展策略
核心素养培养 | 浅谈初中数学教学中学生核心素养的发展策略
-
核心素养培养 | 核心素养背景下初中生数学抽象能力培养策略
核心素养培养 | 核心素养背景下初中生数学抽象能力培养策略
-

学生培养研究 | 初中数学分层作业设计
学生培养研究 | 初中数学分层作业设计
-
学生培养研究 | 基于运算能力培养的初中数学教学实施研究
学生培养研究 | 基于运算能力培养的初中数学教学实施研究
-
学生培养研究 | 基于发展学生核心素养的初中数学单元作业设计研究
学生培养研究 | 基于发展学生核心素养的初中数学单元作业设计研究
-
学生培养研究 | 初中数学探究式教学中培养学生几何作图能力的思考
学生培养研究 | 初中数学探究式教学中培养学生几何作图能力的思考
-
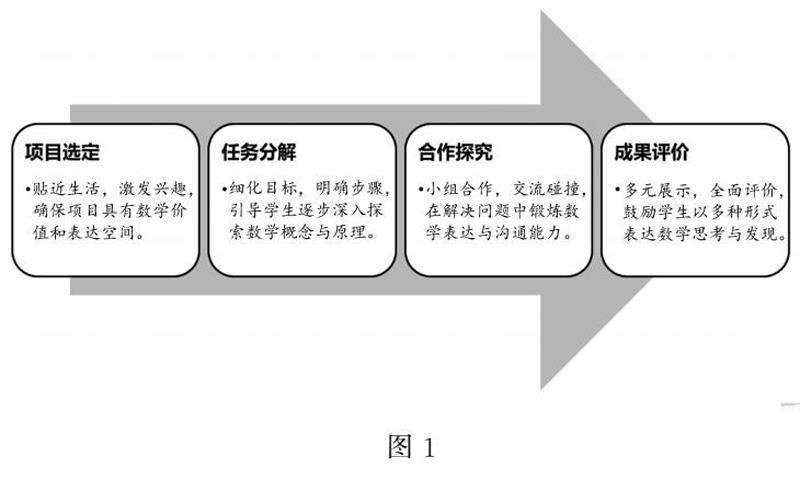
学生培养研究 | 基于项目学习的初中生数学表达能力提升策略
学生培养研究 | 基于项目学习的初中生数学表达能力提升策略
-
学生培养研究 | 盲校初中生数学学习动机与认知策略的关系研究
学生培养研究 | 盲校初中生数学学习动机与认知策略的关系研究
-
学生培养研究 | 初中数学教学中学生自主评价的探索
学生培养研究 | 初中数学教学中学生自主评价的探索
-

教育技术与数学融合 | 信息技术辅助下的初中数学核心素养教学策略研究
教育技术与数学融合 | 信息技术辅助下的初中数学核心素养教学策略研究
-
教育技术与数学融合 | APOS理论下的初中数学几何模型教学设计研究
教育技术与数学融合 | APOS理论下的初中数学几何模型教学设计研究











 登录
登录