全部分类/
教育教学/
高中数理化

高中数理化

2024年19期

北师大集团核心刊物

扫码免费借阅

目录

快速导航

高考　课改 | 透过教材看２０２４年新课标Ⅰ卷

高考　课改 | 透过教材看２０２４年新课标Ⅰ卷

１重视教材例题和基本思想方法
高考　课改 | 素养导向下的创新题命制举隅

高考　课改 | 素养导向下的创新题命制举隅

２０２４年九省联考出现了新定义的创新题，其宗旨是选拔创新人才．教育部一直强调减少机械刷题，回归教材、回归知识的本质，同时强调数学建模，体现高考的公平性与权威性，但是否一定要通过这种高等数学背景来命制新定义的试题呢？笔者进行了如下探究．
高考　课改 | 聚焦主干知识,考查关键能力

高考　课改 | 聚焦主干知识,考查关键能力

１课程标准的学业要求
强基竞赛 | 初等数论中不等式放缩控制方法

强基竞赛 | 初等数论中不等式放缩控制方法

初等数论问题求解，既要用到整除、同余等数论方法，又要用到代数变形、不等式放缩等技巧．这些技巧有助于创设条件、缩小问题范围，并精准追踪目标．本文旨在梳理初等数论中的不等式放缩方法，并展示其在问题求解中的应用．
题根研究 | 探究椭圆中两直线斜率关系为定值时的统一性质

题根研究 | 探究椭圆中两直线斜率关系为定值时的统一性质

圆锥曲线问题是高考数学的热点与难点，过椭圆上一点P 作两条直线分别与椭圆相交于A ，B 两点，设直线PA 的斜率为k１，直线PB 的斜率为k２，当k１与k２的和或乘积为定值时，直线AB 过定点或直线AB 的斜率为定值．本文结合历年的两道高考真题，针对这类问题给出了几种处理方法，希望能对读者有所帮助．
题根研究 | 一道线面平行问题的多角度探究

题根研究 | 一道线面平行问题的多角度探究

证明直线与平面平行是立体几何中经常考查的一类高频问题．在解决这类问题时，首选方法是利用线面平行的判定定理，此外，也可以利用面面平行的性质进行推导，或者利用空间向量法．本文选取一道高考真题进行多角度探究，旨在拓宽解题思路，提高综合应用相关数学知识、方法解题的能力，进一步提升数学核心素养．
题根研究 | 一道关于线面平行的教材习题的探究

题根研究 | 一道关于线面平行的教材习题的探究

立体几何中直线与平面平行的位置关系是非常重要的知识点，本文以人教A 版普通高中教科书数学必修第三册第八章立体几何初步中的一道复习参考题为例，从不同的角度对其进行分析和证明，以期培养学生的直观想象和逻辑推理数学核心素养．
题根研究 | 立体几何中折线长度的最值问题

题根研究 | 立体几何中折线长度的最值问题

立体几何中的最值问题，尤其是折线长度的最值问题是高中数学立体几何的一大难点．对于这类问题，解题的关键是将立体几何问题转化为平面几何问题，通过降维来处理．在处理最值问题时，常用的方法有几何法与代数法．几何法主要是利用几何图形的性质来求最值;代数法则是将几何图形中的最值转化为函数的最值，然后利用函数的性质求解．
题根研究 | 一道正八边形与平面向量交会问题的探究

题根研究 | 一道正八边形与平面向量交会问题的探究

在近几年高考数学中，对平面向量的考查主要以熟悉的平面图形为载体，侧重考查学生的数形结合能力和数学运算求解能力．若试题中涉及“动点”，则目标问题的求解往往有一定难度，能够考查学生分析、解决问题的能力．
考题分类评析 | 两圆公切线模型的探究与应用

考题分类评析 | 两圆公切线模型的探究与应用

两圆的公切线问题是高中数学中的重要知识，也是高考考查的重点内容．本文深入探究了任意位置关系的两圆公切线方程模型，然后巧妙地运用公切线方程模型求解相关问题，实现两圆公切线问题模型化、程序化．
考题分类评析 | 鳖臑模型中的夹角问题

考题分类评析 | 鳖臑模型中的夹角问题

在近几年的立体几何问题中，经常会遇到所给立体图形不易建系、难以计算法向量或综合法论证过于烦琐等问题，从而导致学生无法顺利解决夹角问题．因此，本文根据由特殊到一般的原则，首先，从简单的鳖臑模型入手分析出求二面角的一种新方法，论证出求线面角的最小角定理;然后，将之应用于复杂的立体模型中，从而轻松解决夹角问题;最后，论证出一些有趣的结论．
考题分类评析 | 三角形中的最值问题

考题分类评析 | 三角形中的最值问题

三角形中的最值问题是高考的热点，试题既可考查正弦定理和余弦定理，又可考查三角恒等变换，还可考查基本不等式等内容．因其可利用的公式多、变形技巧强，所以三角形中的最值问题也是难点．下面以最新的各地试题为例，探求三角形中的最值问题的解题策略．
考题分类评析 | 三角函数中一类参数范围问题的求解策略

考题分类评析 | 三角函数中一类参数范围问题的求解策略

三角函数的图像与性质是高中数学的重点知识，也是高考的核心考点，尤其需重点关注三角函数在某区间上的单调性、对称性、零点和极（最）值点个数等问题．本文从６类典型问题入手，探求参数取值范围问题的破解策略，以期达到抛砖引玉、举一反三的目的．
考题分类评析 | 微专题复习视角下例析“立体几何中的动点问题”

考题分类评析 | 微专题复习视角下例析“立体几何中的动点问题”

解决立体几何中动点问题的关键是利用综合法与分析法进行探索，确定动点的轨迹．从考查基础知识、基本方法的角度看，这类问题虽然可以适时地借助向量法解决，但考查的重点往往聚焦于综合应用平面几何与立体几何知识分析问题，其解题过程常伴随着“空间问题平面化”的降维处理方法．
考题分类评析 | 祖暅原理在圆锥曲线中的应用

考题分类评析 | 祖暅原理在圆锥曲线中的应用

祖暅原理作为阅读材料出现在教材（人教A 版普通高中教科书数学必修第二册１２１页的“探究与发现”）中，即“幂势既同，则积不容异”，“势”即是高，“幂”是面积，其基本思想是：若两个几何体在等高处任意方向的横截面积总是相等，则这两个几何体的体积相等．祖暅原理在解决复杂的几何体体积问题时非常有用，尤其是在处理不规则几何体时，常用于由已知几何体的体积推导未知几何体的体积．本文结合部分试题，展示祖暅原理在圆锥
核心考点 | 二项式定理的应用举例

核心考点 | 二项式定理的应用举例

二项式定理是人教A 版普通高中数学教科书选择性必修第三册的一个重要内容，也是高考的核心考点，常以小题的形式出现，主要考查二项展开式的通项、系数和特殊项等问题．解题时要理解二项式的性质，下面对常考题型进行分类求解．
核心考点 | 透析立体几何的变换视角

核心考点 | 透析立体几何的变换视角

立体几何是考查学生空间想象能力的主要载体．立体几何问题的命题视角或求解方法往往涉及几何图形的变换，这些变换主要包括旋转、展开、折叠、补形、分割等．下面举例说明这几种变换方式．
核心考点 | 函数为体,导数为用

核心考点 | 函数为体,导数为用

函数是高中数学的重要板块，也是数学学习能力和数学核心素养的重要载体．在综合题的复习中，要突出函数的本体特征，以函数的具体形式为出发点;科学选择工具辅助分析，合理运用导数研究函数的性质．２０２４年北京市海淀区高三期末测试第２０题，立足于函数自身的特征，要求学生通过对函数形式的分析，逐渐抽丝剥茧，合理转化函数形态，并适当利用导数解决问题．该题以不等式为研究起点、以函数极值为主要研究对象、以曲线切
方法与技巧 | 妙用空间向量法求立体几何动态问题

方法与技巧 | 妙用空间向量法求立体几何动态问题

立体几何中的动态问题是高考常考问题．这类问题涉及三维空间中图形的形状、大小、位置关系等概念，要求学生具备较高的空间想象能力和抽象思维能力．在求解这类问题时，我们常常利用空间向量法，本文重点介绍空间向量法在这类问题中的应用．
方法与技巧 | 探究立体几何最值问题的求解策略

方法与技巧 | 探究立体几何最值问题的求解策略

空间想象、逻辑推理和数学运算等核心素养是高考立体几何的考查目标．立体几何最值问题恰好能考查这三大核心素养，因此此类问题备受命题者青睐．那么求解立体几何最值问题有哪些基本策略？
方法与技巧 | 几何图形中向量数量积最值问题的求解策略

方法与技巧 | 几何图形中向量数量积最值问题的求解策略

求含有平面几何背景的向量数量积的最值问题，是一类常见且重要的问题．这类问题经常与平面向量的模与夹角等知识综合考查，其中与几何图形中有关性质的综合应用比较常见．由于部分学生对这类题型缺乏系统练习，在遇到一些新问题时无从下手．本文列举几道经典的例题，介绍几类常见问题的求解策略，旨在揭示解题规律、探讨解题方法，希望能给读者带来帮助．
方法与技巧 | 猜想的七个角度

方法与技巧 | 猜想的七个角度

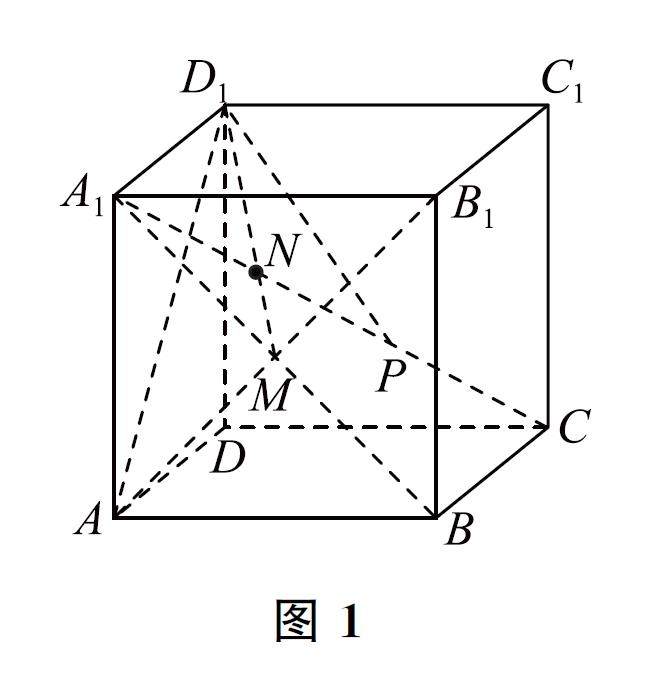
牛顿说过，没有大胆的猜想，就做不出伟大的发现．因此，解题时应大胆猜想，小心求证．猜想是数学家探索数学世界的一种方式、方法，蕴直觉思维与合情推理之神韵，涵探幽索隐与异想天开之妙趣．数学猜想是推动数学发展的重要动力，是创造性思维的一种方式．可如何巧妙地、数学地猜想，才能使得猜想有“法”、有“招”，极具探究价值？本文尝试从七个角度出发，巧妙猜想，先猜后证，猜证合一，赋烦琐以简洁有趣，予枯燥以生动奇巧．
方法与技巧 | 动态立体几何问题中的“动中寻定”

方法与技巧 | 动态立体几何问题中的“动中寻定”

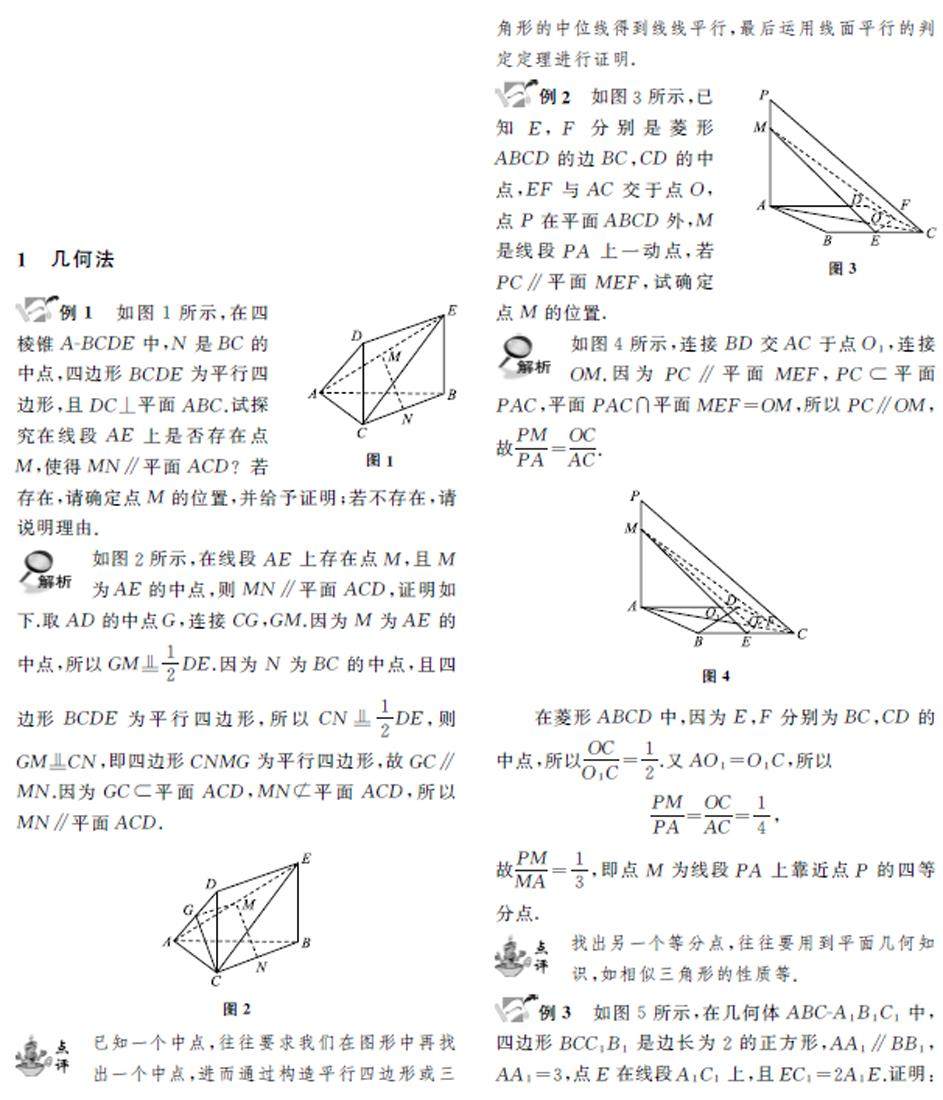
在空间几何体中，由于点、线、面位置的不确定引起的距离、角度、面积、体积的变化问题，我们称为动态问题．这类问题在高考中常以选择题或填空题的形式出现，能有效考查学生的知识综合应用能力、推理论证以及空间想象能力．解决此类问题的一种重要策略是从动量中寻找不变量，即动中寻定，其中主要涉及寻找定点、定线、定面或定体，下面举例分析．１定点动态立体几何问题常见的题型有求角度的取值范围、距离的最值等，这
方法与技巧 | 剖析立体几何线面平行证明方法

方法与技巧 | 剖析立体几何线面平行证明方法

立体几何是高中数学的核心内容，也是高考的重要考点．它主要研究空间几何体的结构以及点、线、面之间的位置关系．通过立体几何的学习，可以培养学生的空间想象和逻辑推理能力．有关线面平行问题虽然属于基础题，但其解法多样、解题思路广阔，值得细细品味和深入研究．那么这类问题的常用解法有哪些呢？本文举例说明．
方法与技巧 | 不建系向量法求解立体几何问题

方法与技巧 | 不建系向量法求解立体几何问题

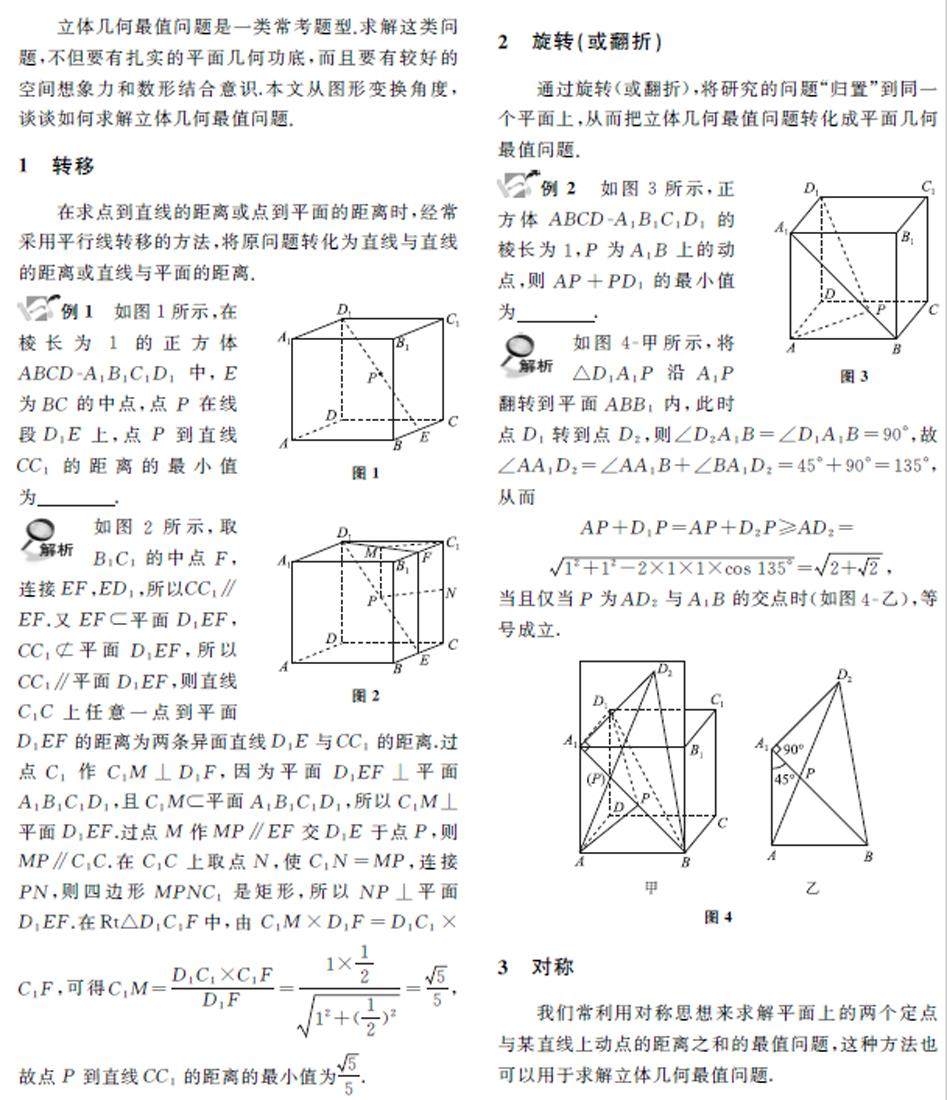
立体几何作为高中数学的重要内容，在高考中占据重要地位，特别是与二面角有关的问题更是深受高考命题者的青睐．这类问题比较抽象，对学生的空间想象能力要求较高，因而对部分学生而言具有一定的挑战性．在求解这类问题时，学生可考虑运用不建系向量法．不建系向量法是一种不需要建立坐标系，仅通过向量运算求解问题的方法．
方法与技巧 | 巧用图形变换,妙求“立几”最值

方法与技巧 | 巧用图形变换,妙求“立几”最值

立体几何最值问题是一类常考题型．求解这类问题，不但要有扎实的平面几何功底，而且要有较好的空间想象力和数形结合意识．本文从图形变换角度，谈谈如何求解立体几何最值问题．
方法与技巧 | 动态分析,妙求取值范围

方法与技巧 | 动态分析,妙求取值范围

求参数的取值范围问题是高中数学较为常见的题型，求解这类问题的主要方法有分类讨论法、参变量分离法和数形结合法．数形结合法也称图像法，用该方法求解这类问题通常需要构造两个函数，一个不含参数，另一个含参数．先作出不含参数的函数图像，再通过含参数的函数图像的动态变化来直观确定参数的取值范围，这就是动态分析，本文举例说明．

过往期刊

更多

猜你喜欢

龙源综合阅览室V1.0