全部分类/
教育教学/
高中数理化

高中数理化

2025年10期

北师大集团核心刊物

扫码免费借阅

目录

快速导航

名师工作室 | 祖恒原理：跨越千年的几何智慧，照亮体积计算的航道

名师工作室 | 祖恒原理：跨越千年的几何智慧，照亮体积计算的航道

1祖恒原理的数学史发展祖晅原理是中国古代数学史上的重要成就，其发展脉络也是球体体积公式的发现过程. 1. 1 《九章算术》中的公式《九章算术》中记载：置积（立方）尺数，以十六乘之，九而一，所得开立方除之，即立圆径.相当于给出了已知球的体积 V 求球的直径的公式，即 d = 3根号下 1 6／ 9V球，则V球 = 9／ 1 6} d 3 1.2刘徽的发现与牟合方盖魏晋时期，数学家刘
突破重难点 | 立足基础探寻规律

突破重难点 | 立足基础探寻规律

直线与圆相结合的问题是高考的重要考查知识点，逐步成为近几年的高考热点题型.解题的核心在于探讨点、直线与圆之间的相互关系，深人分析点与圆之间的距离、直线与圆的交点情况以及圆在平面中的位置，这对逻辑推理能力有着较高的要求.本文分析一些热门题型，旨在剖析并优化解题路径. 1 弦长问题在求解直线与圆的弦长问题时，常用的方法是几何法.首先依据直线和圆的方程绘制出相应的图形，并通过圆的方程确定圆心的位置
突破重难点 | 导数的几何意义应用解密

突破重难点 | 导数的几何意义应用解密

导数的几何意义，即导数值表示曲线 y = f （ x ）在点处切线的斜率，其充分体现了数与形的完美结合.切线问题主要考查导数的几何意义，具有一定的综合性.纵观近十年的高考试题，可以发现曲线的切线问题是考查的一大热点.基于此，本文借助导数的几何意义，对高考试题的考查方向进行分类解析. 1单切线问题单切线问题是指一个函数图像的切线问题，主要包括在某点处型、过某点型和参数的值或取值范围型
突破重难点 | 琴生不等式的教材溯源及其应用

突破重难点 | 琴生不等式的教材溯源及其应用

琴生不等式是数学中一个重要的不等式，它描述了凸（凹）函数在数值平均与函数平均之间的不等式关系，在证明不等式和处理凸（凹）函数相关问题中有着广泛的应用 1琴生不等式的教材溯源琴生不等式在高中阶段是没有作具体要求的，因为它是高等数学研究函数的重要工具.虽然高中阶段没有对它作具体要求，但它的身影却出现在教材中. 引例（人教A版普通高中教科书数学必修第一册第101页第8题，节选）若，证明：
突破重难点 | 拓广探索教考衔接

突破重难点 | 拓广探索教考衔接

¹²（1.2.） 2025年高考综合改革适应性测试（以下简称2025年八省联考）高中数学试题由教育部统一命制，主要是针对第五批高考综合改革的八个省、自治区进行的一次大规模的调研考试.2025年八省联考具有影响力大、权威性高、导向性强等特点.深入研究2025年八省联考试题具有一定的理论价值与实践意义，能为2025届高三师生备战高考提供方向性指引.基于此，本文聚焦2025年八省联考第10题，对试题进
突破重难点 | 传承中考查“四层四翼” 创新中落实核心素养

突破重难点 | 传承中考查“四层四翼” 创新中落实核心素养

近五年高考数学卷中全面考查了解三角形的基本知识，命题方式新颖别致，紧扣《中国高考评价体系》中的“一核、四层、四翼”，试题体现《普通高中数学课程标准（2017年版2020年修订）》中提出的数学运算、逻辑推理、直观想象和数学建模等数学核心素养. 1近五年高考数学中解三角形试题考点透析笔者研究发现，近五年高考数学中部分解三角形试题所考查的知识点、题型和核心素养详细情况统计如表1所示. 表1 从
突破重难点 | 2024年高考数学新课标I、Ⅱ卷圆锥曲线试题的变式训练研究

突破重难点 | 2024年高考数学新课标I、Ⅱ卷圆锥曲线试题的变式训练研究

2024年新课标卷对解析几何部分的考查突出基础性、综合性、创新性，凸显数学本质，对学生的数学运算、逻辑推理、直观想象等数学学科核心素养有极好的检测功能.本文深度分析2024年高考解析几何部分试题，以期帮助学生看清试题考查的数学本质. 1注重探究方法，突出创新性考查例1 （2024 年新课标I卷11，多选题）设计一条美丽的丝带，其造型可以看作图1中曲线 C 的一部分.已知 C 过坐标原点 O
突破重难点 | 赏析与数字2025有关的数学题

突破重难点 | 赏析与数字2025有关的数学题

数学题的命制离不开数字，将当年的年份巧妙编进高考试题不但能使数学题产生年代感，而且也增添几分趣味.时值2025年，与数字2025有关的数学新题应运而生，本文分类列举几道例题，与大家共赏. 1抽象函数的函数值问题例1 已知定义在上的函数 f （ x ）满足且对任意的 x ， y ∈ R， f （ x + y ） = f （ x ） f （ 1 - y ） + f （ y ） f （ 1
突破重难点 | 对一道解三角形“正切比模型”问题的探及思考

突破重难点 | 对一道解三角形“正切比模型”问题的探及思考

在高三复习备考中，学生不应局限于对题自的具体解答和重复训练，而应对问题进行深层次的探究及引申，充分挖掘题目的内涵和外延，用更高的观点去看待问题.本文以一道“正切比模型”问题为例，阐述它的解法探究、解法辨析、一般化推广及试题迁移.2025年湖南省常德市高三一模数学第16题就是一道“正切比模型"问题，笔者先对其从多种视角进行解法探究，对条件进行转化，再比较不同解法的特点，从而总结出求解此类问题的通
突破重难点 | 从定比分点的视角看解三角形

突破重难点 | 从定比分点的视角看解三角形

解三角形作为高中数学的重要内容，在高考中占有重要的地位，所以对三角形各种性质的研究是学生日常学习的重点.“奔驰定理”的常规认识是通过向量的角度并结合三角形重心的性质推导得出的，本文从定比分点的视角，对“奔驰定理”进行探究，以期帮助学生对三角形的性质形成进一步的认识.对于平面上的任意一个三角形，它的“四心”（即重心、内心、垂心和外心，它们分别是三角形三条中线、三条角平分线、三条高线、三条垂直平分线的
突破重难点 | 高考“思维型”试题及分类解析

突破重难点 | 高考“思维型”试题及分类解析

高考数学历来重视创新命题情境和对数学思维的考查，2025年1月9日教育部为第五批高考改革试点的八个省、自治区（河南、陕西、山西、四川、云南、青海、宁夏、内蒙古）命制了2025年高考综合改革适应性测试（以下简称2025年八省联考）.2025年八省联考数学第11题是一道“思维型"试题.所谓“思维型"试题指的是不受中学数学教材中知识点的束缚，与中学数学的固有知识和模型没有直接和必然联系的一种全新形式的创
突破重难点 | 2024年高考数学新课标1卷第13题解析与变式训练

突破重难点 | 2024年高考数学新课标1卷第13题解析与变式训练

导数的几何意义以及平面解析几何的核心知识，是高考的高频考点.2024年高考数学新课标I卷的第13题聚焦该考点考查两条曲线的公切线问题，该题题型多变、解法灵活且具有显著的区分度.为加深学生对这类题型的理解，本文以该题为例，进一步对其进行变式训练，旨在助力学生全面、深入地掌握相关问题的解题要领， 1真题再现例1（2024年新课标I卷13）若曲线在点（0，1）处的切线也是曲线的切线，则 a
突破重难点 | 聚焦高考常见二项式定理相关题型的深度剖析

突破重难点 | 聚焦高考常见二项式定理相关题型的深度剖析

二项式定理是高中数学的重要内容，也是高考数学考查的重点内容，在试卷中占有一定分值.在历年高考中，二项式定理常以客观题的形式出现，并且相关试题的命题风格与考查方向相对稳定.本文深入剖析与二项式定理相关的常见题型. 1求二项式展开式中的特定项及相关量在二项展开式中，常常会出现诸如常数项、有理项、整式项以及系数最大的项等特殊项.求解这些特殊项的关键在于借助二项展开式的通项公式 .通过分析题目所
突破重难点 | 对教材一个公式的理解、拓展与应用

突破重难点 | 对教材一个公式的理解、拓展与应用

教材是知识的载体，教材中的每一道例题和习题都具有极高的价值.总览近几年数学高考试题，大多数试题都能在教材中找到“原型”，它们或是“原型”的变式题，或是“原型”的适度拓展引申题.因此应该重视教材例题、习题的学习与研究，尤其是对学生解题大有帮助的二级结论.基于此，本文对教材例题中的重要结论"tanA十tanB十tan C = tan A tan B tan C ；的理解、拓展与应用进行探讨. 1理解
突破重难点 | 需要重视的命题新动向

突破重难点 | 需要重视的命题新动向

《普通高中数学课程标准（2017年版2020年修订）》虽未明确指出对反函数的考查要求，但从教材内容来看，对于反函数的学习，学生需要掌握函数 y = 与互为反函数以及反函数的定义域和值域分别是原函数的值域和定义域等知识.教材配套的习题也对这些知识进行了练习巩固. 如果仅从人教A版普通高中教科书数学必修第一册第134页关于反函数的叙述和习题来判断，认为反函数的考试要求很低，那就错了. 从教材
突破重难点 | 正态分布问题的重点题型及求解对策

突破重难点 | 正态分布问题的重点题型及求解对策

正态分布问题是概率统计中比较重要的组成部分，由于其自身的特点以及在实际生活中应用广泛，已越来越受到高考命题专家的青睐.为确保全面掌握题型变化并实现解题过程的完整性，有必要深入剖析其核心题型特征并构建系统化解题策略.基于此，本文系统梳理该类问题的重点题型，精准定位高频考点. 1熟悉正态曲线例1 图1是三个正态分布密度函数的图像，下列结论中正确的是（）. 图1 A. （204号 B
突破重难点 | 探究三角形两边比值的取值范围

突破重难点 | 探究三角形两边比值的取值范围

1 引例题目在△ABC中，角 A ， B ， C 的对边分别为，且 B C 边上的高为 a，则的最大值为（）. A.8 B.6 C.32 D.4 解析因为 B C 边上的高为，所以则 .由余弦定理得整理得即 .因为 A ∈ （ 0 ， π ），所以 A + 当即时， 4 sin （ A + 取得最大值4，所以的最大值为4，故选D
方法与技巧 | 指向数学新高考的考前攻略

方法与技巧 | 指向数学新高考的考前攻略

2025年高考已悄然临近，本文针对新高考背景下的数学复习备考，给出一些考前复习策略与应对方法，供读者参考. 1 回归教材，夯实基础从2024年的九省联考、高考到2025年的八省联考来看，新高考数学意在引导高中数学教学遵循课程标准，夯实学生学习基础，重视教材，助力减轻学生学业负担.试题考查内容主要涉及“函数”“几何与代数”“概率与统计”三大主题的知识内容，突出对数学运算和逻辑推理等数学学科核心
方法与技巧 | 从知识方法到思维品质

方法与技巧 | 从知识方法到思维品质

1 引言《普通高中数学课程标准（2017年版2020年修订）》要求高考命题中应特别关注数学学习过程中思维品质的形成.衡量一个人的思维品质主要包括广阔性、深刻性、敏捷性、灵活性、独创性和批判性，这六个维度共同塑造了一个人的思维品质进阶路线（如图1），其中广阔性与深刻性是思维品质的根基，它代表知识方法理解层面的厚度；敏捷性与灵活性是思维品质的树干，它决定问题分析应变层面的速度；独创性与批判性是思维
方法与技巧 | 在高考命题视角下，探讨直观想象核心素养的落实及应对策略

方法与技巧 | 在高考命题视角下，探讨直观想象核心素养的落实及应对策略

直观想象是高中数学学科六大核心素养之一，在《普通高中数学课程标准（2017年版2020年修订）》（以下简称《课程标准》）中，对高考命题建议指出：高考命题要注重对学生数学学科核心素养的考查.在命题中，选择合适的问题情境考查数学学科核心素养，每道题需要给出反映相关数学学科核心素养的水平划分依据.核心素养水平分为三级：一级是在熟悉的情境中考查直观想象，二级是在数学知识的关联情境中考查直观想象，三级是在综
方法与技巧 | 高考数学选择题和填空题常规解题方法及技巧点拨

方法与技巧 | 高考数学选择题和填空题常规解题方法及技巧点拨

随着高考新一轮改革的进行，数学试题的选择题、填空题由原来“ 8 + 4 + 4 ”模式变成了现在的“ 3 + 3 模式，分值也由原来的80分变成了现在的73分，虽然分值有所减少，但这仍然占据了卷面分值的半壁江山.高考数学的选择题和填空题只需要选择选项和填写结果，如何以最少的时间“快”“准”“狠”地解题，真正做到“小题小做，小题巧做”，进而成功解题？接下来文章对高考数学选择题和填空题常规解题思想方
方法与技巧 | 从函数的几何特征入手寻求导数的破题之法

方法与技巧 | 从函数的几何特征入手寻求导数的破题之法

在北京高考数学命题中，导数问题已突破传统知识考查的边界，成为检验学生多维能力的关键载体本文以一道经典导数题目为例，对该题进行多角度分析，以期为学生复习备考提供有益的参考. 1 试题呈现题目已知函数，曲线 f （ x ）在（ - 1 ， f （ - 1 ））处的切线方程为 y = - x - 4 （1）求的值；（2）求证： f （ x ）只有一个零点；（3）记 f （
方法与技巧 | 观察分析适当转化多想少算提升思维

方法与技巧 | 观察分析适当转化多想少算提升思维

高中数学作为一门重要的基础学科，在培育学生逻辑思维、抽象思维以及创新思维方面发挥了重要作用.然而，审视当前学生学习现状，不难发现学生常常深陷大量机械性的计算练习之中，过度关注运算结果，却严重忽视了对数学问题内在本质的深度观察与精准分析，进而阻碍了自身思维能力的有效提升. 数学教育的目标不仅是让学生掌握知识和技能，更重要的是培养学生独立思考和解决问题的能力.传统重计算轻思维的学习模式已难以满足现
方法与技巧 | 数学解题的根基：轨迹意识与动态思维

方法与技巧 | 数学解题的根基：轨迹意识与动态思维

在许多变化的几何问题中，用动态化视角分析静态化的数学背景，有时能从试题背景中挖掘到蕴藏“动点运动轨迹”的思维顿悟点.运用这种动态数学思维解决问题，可以优化解题过程，发散数学思维.基于此，本文结合典型的试题，溯源归纳出6种类型的轨迹背景，并体会树立“轨迹意识"在解题中的价值意蕴，例1设向量满足 ,若存在实数 λ ，使得，则向量与的夹角不等于（）. A. B.60° C.12
方法与技巧 | 立体几何考题分析及备考建议

方法与技巧 | 立体几何考题分析及备考建议

2024年新课标I卷与新课标Ⅱ卷在立体几何方面的命题风格仍保持稳定，其核心考点是几何体表面积与体积、线面关系、线面角与二面角等，试题均以学生熟悉的棱锥、棱台、圆柱等图形为背景，难度整体分布在高、中、低档各个区间，既能考查学生的直观想象、逻辑推理、空间思维等核心素养，又有一定的区分度.本文对试题进行分析，并提出几点备考建议， 1命题导向与试题评析 1.1立足教材，考查基础知识随着高考的不断改
方法与技巧 | 从教材习题谈谈飘带函数及其应用

方法与技巧 | 从教材习题谈谈飘带函数及其应用

教材习题是高考复习备考的重要资料，挖掘习题的价值、回归教材是提高复习备考效率的重要环节.本文对一道教材习题进行多角度分析，探究出了几个一般性的性质，希望能为学生复习备考提供参考. 1 问题的提出题目（人教A版普通高中教科书数学必修第一册 101页复习参考题3第12题)试讨论函数 y = x - 的定义域、值域、单调性、奇偶性，并画出函数图像. 容易得出上述习题答案，但是对于一般的函数，它
方法与技巧 | 归教材探题根寻解法谈“衔接”

方法与技巧 | 归教材探题根寻解法谈“衔接”

《普通高中数学课程标准（2017年版2020年修订）》（以下简称《课标》和《中国高考评价体系》指出，高考试题命制的原则是“源于教材，又高于教材”.对于这一要求，2025年高考综合改革数学适应性测试试卷落实得很到位，此次的数学适应性测试题是由教育部教育考试院命制的，该套试卷依据“依标命题、源于教材"的命题理念，强化与《课标》教材衔接.本文通过回归教材，探究本套试卷中第18题的题源及解法. 1 归教
方法与技巧 | 解析几何中关于三角形“四心”问题探究

方法与技巧 | 解析几何中关于三角形“四心”问题探究

三角形的“四心"是指三角形的重心、垂心、内心、外心.解析几何中时常出现有关“四心”的问题，这也体现了平面几何与解析几何密切相关.解决此类问题不但需要熟练掌握解析几何问题的求解策略，还需要注重三角形“四心"的特点与应用.本文通过典型例题的分析点评，介绍“四心”问题的解题思路和技巧. 1关于三角形重心问题重心是三角形三条中线的交点，重心到三角形顶点的距离是它到对边中点距离的两倍.求解三角形重心问题
方法与技巧 | 警惕点差法“失效”

方法与技巧 | 警惕点差法“失效”

在直线与圆锥曲线问题中，学生有时会遇到一类中点弦问题.解决这类问题常采用点差法，点差法可以巧妙地将斜率公式、中点坐标公式结合起来，减小计算量，提高解题速度，因此它具有很好的推广价值和实用性.在使用点差法求解涉及双曲线的“中点弦”问题时，常常会出现“中点弦"时而存在，时而又不存在的情况.本文通过对教材一道习题的分析，探究“中点弦"不存在的原因，给出运用数形结合思想快速判断"中点弦”是否存在的方法，同
方法与技巧 | 高考数学临场答题技巧分享

方法与技巧 | 高考数学临场答题技巧分享

高考对大多数学生来说是人生的重要节点，三年的学习固然重要，但临场发挥的作用也不容忽视.正所谓“养兵千日，用兵一时”，如何在高考中发挥出自己的潜力，这就需要掌握一定的实战技巧. 1时间分配要科学合理高考通常会提前5分钟发放试卷，利用这段时间检查试卷的完整性，对考题类型、考点分布等做到心中有数.一套高考数学试卷近20道题目，题型包括单选题、多选题、填空题、解答题，考试时间120分钟，针对不同的题
方法与技巧 | 高考数学考前30天冲刺计划

方法与技巧 | 高考数学考前30天冲刺计划

随着高考的临近，有些考生不知该如何利用好考前30天，甚至有的考生认为大局已定.其实只要做好计划，按计划充实度过每一天，一定会有意想不到的收获.那么应该如何做，才能百尺竿头，更进一步？笔者制订了如下30天冲刺计划，供考生参考. 1确定目标，做到自我突破首先要做的是明确冲刺的目标，有的考生需要做的是巩固基础，这里所说的基础不仅包括基本概念、基本性质、基本公式原理，还包括常考题型、常用方法等.以抛
方法与技巧 | 基于高考新情境选择压轴题的题型剖析与求解策略

方法与技巧 | 基于高考新情境选择压轴题的题型剖析与求解策略

本文围绕高考数学新情境选择压轴题展开，详细剖析以新概念、新运算、新性质、新背景、新公式为背景的题型.通过典型例题解析，总结解题思路与方法，并给出备考建议，旨在助力学生攻克此类难题，提升备考效率. 1引言近年来，选择压轴题巧妙地融入新概念、新运算、新性质、新背景、新公式等元素，全面考查学生的数学抽象、逻辑推理、数学运算等数学学科核心素养，深入探究此类题型，对学生精准把握高考命题规律，有效提升解
方法与技巧 | 解透一题拓广探究触类旁通回归本质

方法与技巧 | 解透一题拓广探究触类旁通回归本质

什么是外接球？若几何体的所有顶点都在一个球的球面上，则称这个球为该几何体的外接球.外接球半径是指球心到多面体任意一个顶点的距离.立体几何的外接球是立体几何模块重要内容，也是高考热点问题，这类问题蕴含着极其重要的数学思想和方法，对知识、方法、技能考查丰富，对逻辑推理、空间想象、数学建模、数学运算等数学学科核心素养考查全面，具有很好的探究价值.本文以2025年八省联考第19题第（1）问为例，与大家交流
方法与技巧 | 聚焦平面向量中的取值范围(最值)问题

方法与技巧 | 聚焦平面向量中的取值范围(最值)问题

平面向量中的最值问题在高中数学中颇为常见，它融合了多个知识点，是数学知识体系的一个重要交会点.这类问题通常综合考查学生对平面向量定义、性质、定理及运算法则的掌握情况和应用能力.平面向量背景下的最值问题，因其综合性强、涉及知识点广泛、解法灵活多变而备受关注.本文通过具体例子探讨平面向量取值范围（最值）问题的求解策略，以期帮助学生提升解题能力. 1代数式（参数）的取值范围（最值）问题求解有关代数
方法与技巧 | 利用零点存在定理探索零点问题的取点策略

方法与技巧 | 利用零点存在定理探索零点问题的取点策略

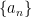
零点问题（包括极值点问题）是函数与导数的核心问题，常出现在近几年的高考试题中.此类问题虽然难度较大，技巧性较强，但实际上有其基本规律和通性通法.解决此类问题时，利用零点存在定理来分析函数零点的个数是一种常见的解题思路，但学生往往难以掌握其中的技巧.在运用零点存在定理解题时，如何确定取点的区间（两点异号）是解决此类问题的关键，也是难点.文章浅谈取点的基本原理，给出零点问题取点的四个视角. 1 巧取
方法与技巧 | 例谈高考数列不等式证明中通项放缩的策略

方法与技巧 | 例谈高考数列不等式证明中通项放缩的策略

数列是高中数学的重要内容，也是高等数学研究极限的重要载体，是初等数学和高等数学的重要衔接点，更是各地高考中的热点和难点，而数列不等式的证明更是难点中的难点.此类问题所对应的数列一般不能直接求和，通常需要对通项或求和后的结果进行适当变形放缩后才能求和.放缩法的基本思想是通过放缩将原本不能求和的数列变成可以求和的数列.下面将结合具体例题分类归纳放缩的策略. 1放缩成等差数列求和若数列的通项公
方法与技巧 | 例谈柯西不等式在高中数学解题中的应用

方法与技巧 | 例谈柯西不等式在高中数学解题中的应用

（人教A版普通高中教科书数学必修第二册习题6.3第16题）用向量方法证明：对于任意的，d ∈ R ，恒有不等式上述习题中的不等式是二维柯西不等式.柯西不等式是高中数学中的经典不等式之一，也是高中数学不等式版块的必备知识.n 维柯西不等式：对于任意的实数及，有当且仅当存在常数 λ 使得时，等号成立.高考中也经常考查二维柯西不等式和三维柯西不等式的应用，以下结合具体
方法与技巧 | 三点共线问题背景下三角形中线段的交点问题探究

方法与技巧 | 三点共线问题背景下三角形中线段的交点问题探究

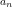
1三角形中的第一个性质性质1 在△ABC中，已知 1），与 C E 交于点 P ，且，则证明如图1所示，由条件可得图1 因为 C， P， E 三点共线，所以即值得一提的是，该性质的应用过程中， x ， y 的取值要准确，即从单独的点 A 出发， y AB. 2 性质1的应用例1如图2所示，在Δ A B C 中，已知段 A D 与 B
方法与技巧 | 已知递推关系求通项an的几种技巧

方法与技巧 | 已知递推关系求通项an的几种技巧

在高中阶段，等差数列与等比数列是数列模块的学习重点.在已知递推关系求解通项公式的过程中，常利用构造法将问题转化为等差数列或等比数列问题.在这一过程中，学生既要掌握数列的基础知识，又要分析题目所给条件，准确识别数列的类型. 1待定系数法型数列例1已知数列满足 2，求的通项公式. 因为，所以 1）.又，所以是以9为首项、3为公比的等比数列，即，故在探讨
方法与技巧 | 谈图示法在概率学习中的工具性作用

方法与技巧 | 谈图示法在概率学习中的工具性作用

本文针对人教A版高中数学教材中概率部分的内容展开深人探究，以树状图、表格和Venn图三种图示法为工具，系统梳理并提炼出应对三类典型概率问题的策略. 1概率学习在教材中的地位和价值概率是高中数学的重要内容，被编排在必修第二册和选择性必修第三册.在概率的学习过程中，教材必修第二册将树状图、表格、Venn图等图示法作为工具穿插其中，使学生能很好地理解样本点、随机事件、样本空间、互斥事件、独立事件等
方法与技巧 | “抓住”角平分线实质快速求解三角形问题

方法与技巧 | “抓住”角平分线实质快速求解三角形问题

在解三角形问题中，如果已知三角形中的一个内角的平分线或能够推出某内角的平分线，则应充分挖掘其他条件与此条件的内在关系，并“抓住"其特点建立相关等式求解问题.本文结合典型例题介绍解三角形问题的常用解题技巧， 1“抓住”两个角相等例1在 Δ A B C 中，内角 A ， B ， C 的对边分别是，若 Δ A B C 的三条角平分线相交于点 O ，且的面积为（204号，求 0 因为
方法与技巧 | 解析几何问题简化计算策略

方法与技巧 | 解析几何问题简化计算策略

解析几何问题的求解是一个复杂且烦琐的过程，其中包含着大量的字母运算与代数变形，如果处理不当就会对解题造成很大困难.因此，在研究其解题思路、探讨常规方法的同时，深化对简化计算方法的研究很有必要，下面举例介绍四种简化计算的策略， 1巧用定义，揭示本质数学定义堪称性质之源，奠定了其他相关知识的基石.解题时应重视运用圆锥曲线的定义以及数形结合思想，进行定量分析与定性判断. 例1已知双曲线 E 的
方法与技巧 | 站在《课程标准》的视角谈2025年平面向量备考

方法与技巧 | 站在《课程标准》的视角谈2025年平面向量备考

《普通高中数学课程标准（2017年版2020年修订）》（以下简称《课程标准》对平面向量的考查要求主要包括平面向量的概念、几何运算与坐标运算、平面向量基本定理以及平面向量的应用.从近年高考试卷来看，平面向量的考题均围绕《课程标准》的要求展开.本文站在《课程标准》的视角，对2025年平面向量模块的备考提出几点看法，供考生参考. 1准确理解向量概念向量是既有大小又有方向的量，大小即为向量的模.模相
强基计划 | 例析不等式的证明策略

强基计划 | 例析不等式的证明策略

不等式是高中数学的重要内容.近几年的数学强基竞赛中经常出现以不等式为背景的证明题，尤其是结构具有一定对称形式的不等式，它全面考查学生对重要不等式、基本不等式、柯西不等式，乃至琴生不等式等掌握的熟练程度，因而综合性大、灵活性强.本文结合部分不等式证明题的解答，揭示一些不等式的基本证明策略，希望能为读者提供思路和帮助. 1典例剖析例1 已知正数满足 a + b + c + d = 1 求证：
高考模拟 | 2025年普通高等学校招生全国统一考试模拟试卷数学(新课标I卷）

高考模拟 | 2025年普通高等学校招生全国统一考试模拟试卷数学(新课标I卷）

（江西省江西师范大学瑶湖校区）（本试卷满分150分，考试用时120分钟）一、单选题（本题共8小题，每小题5分，共40分.在每小题给出的选项中，只有一项是符合题目要求的.） 1.已知复数（i为虚数单位），则 A. 2 2.2025 年春节期间，国产电影《哪吒之魔童闹海》凭借其震撼的特效、生动的情节与深刻的思想票房一路攀升.截至2025年2月6日登顶中国影史票房冠军.下表为某平台
高考模拟 | 2025年普通高等学校招生全国统一考试模拟试卷数学（新课标Ⅱ卷)

高考模拟 | 2025年普通高等学校招生全国统一考试模拟试卷数学（新课标Ⅱ卷)

（本试卷满分150分，考试用时120分钟）一、单选题（本题共8小题，每小题5分，共40分.在每小题给出的选项中，只有一项是符合题目要求的.） 1.复数为虚数单位）的模为（）. A .1 B .根号下 2 C .根号下 3 D .2 2.设集合A={|是小于10的自然数），B={|χ²+x-6<0），C={x|1> 1>1}，则A∩（BUC）=（： A.
高考模拟 | 2025年普通高等学校招生全国统一考试模拟试卷数学(北京卷)

高考模拟 | 2025年普通高等学校招生全国统一考试模拟试卷数学(北京卷)

（本试卷满分150分，考试用时120分钟）一、选择题（本题共10 小题，每小题4分，共40分.在每小题给出的四个选项中，只有一项是符合题目要求的.）1.已知集合，则： A. （ - 2 ， 0 ） B.（0，2） C.（-2，3） D.（2，3） 2.复数（i是虚数单位）的虚部是（）. 3.下列函数中，是偶函数且值域为的是（）. 4.已知向量，其中
高考模拟 | 2025年普通高等学校招生全国统一考试模拟试卷数学（天津卷)

高考模拟 | 2025年普通高等学校招生全国统一考试模拟试卷数学（天津卷)

（本试卷满分150分，考试用时120分钟）一、选择题（本题共9小题，每小题5分，共45分.在每小题给出的四个选项中，只有一项是符合题目要求的.）1.设全集，集合，，则 A. B. C.{3，4} D.{2，3，4，5} 2.设 a b∈R ，则“ ∣ a ∣ > ∣ b ∣ ”是“ a + b ≠ 0 的（）. A.充分不必要条件 B.必要不充分条件 C.充

过往期刊

更多

猜你喜欢

龙源综合阅览室V1.0